Intersecting Chords Form A Pair Of Congruent Vertical Angles
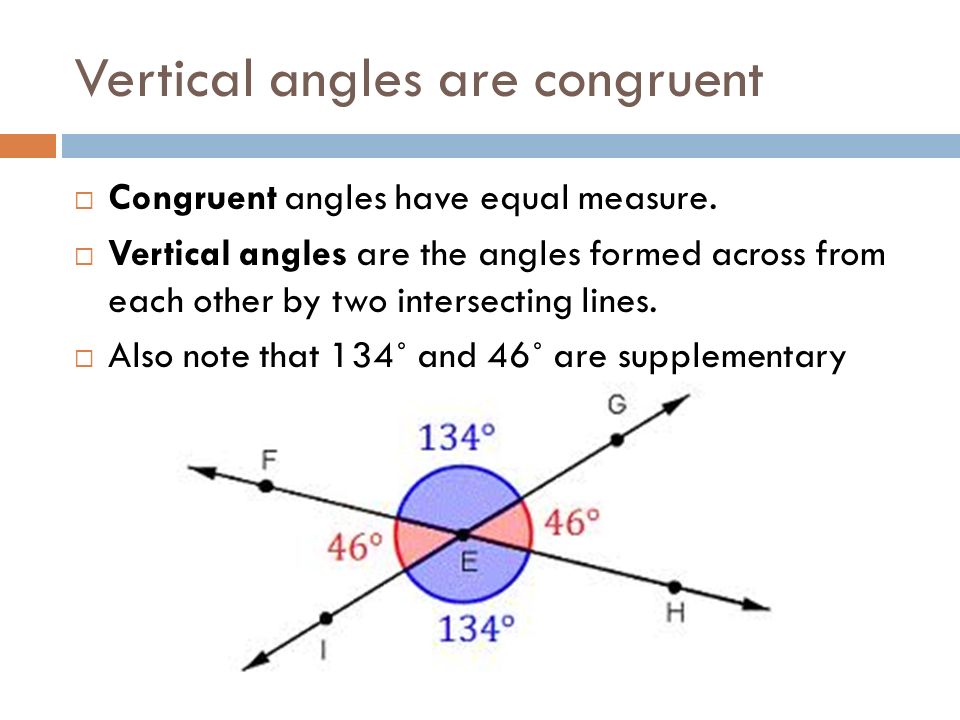
Intersecting Chords Form A Pair Of Congruent Vertical Angles - Intersecting chords form a pair of congruent vertical angles. In the diagram above, ∠1 and ∠3 are a pair of vertical angles. Any intersecting segments (chords or not) form a pair of congruent, vertical angles. A chord of a circle is a straight line segment whose endpoints both lie on the circle. ∠2 and ∠4 are also a pair of vertical angles. Web i believe the answer to this item is the first choice, true. Intersecting chords form a pair of congruent vertical angles. Are two chords congruent if and only if the associated central. Thus, the answer to this item is true. Vertical angles are the angles opposite each other when two lines cross.
A chord of a circle is a straight line segment whose endpoints both lie on the circle. Web if two chords intersect inside a circle, then the measure of the angle formed is one half the sum of the measure of the arcs intercepted by the angle and its vertical angle. Intersecting chords form a pair of congruent vertical angles. Any intersecting segments (chords or not) form a pair of congruent, vertical angles. Thus, the answer to this item is true. Web do intersecting chords form a pair of vertical angles? In the diagram above, chords ab and cd intersect at p forming 2 pairs of congruent vertical angles, ∠apd≅∠cpb and ∠apc≅∠dpb. Are two chords congruent if and only if the associated central. Web intersecting chords theorem: If two chords intersect inside a circle, four angles are formed.
Not unless the chords are both diameters. Thus, the answer to this item is true. Vertical angles are the angles opposite each other when two lines cross. Vertical angles are formed and located opposite of each other having the same value. What happens when two chords intersect? Intersecting chords form a pair of congruent vertical angles. A chord of a circle is a straight line segment whose endpoints both lie on the circle. Since vertical angles are congruent, m∠1 = m∠3 and m∠2 = m∠4. How do you find the angle of intersecting chords? That is, in the drawing above, m∠α = ½ (p+q).
Explore the properties of angles formed by two intersecting chords. 1
That is, in the drawing above, m∠α = ½ (p+q). Thus, the answer to this item is true. Web if two chords intersect inside a circle, then the measure of the angle formed is one half the sum of the measure of the arcs intercepted by the angle and its vertical angle. Additionally, the endpoints of the chords divide the.
Intersecting Chords Form A Pair Of Supplementary Vertical Angles
Web intersecting chords theorem: If two chords intersect inside a circle, four angles are formed. Vertical angles are the angles opposite each other when two lines cross. In the diagram above, ∠1 and ∠3 are a pair of vertical angles. Any intersecting segments (chords or not) form a pair of congruent, vertical angles.
Math 010 Chapter 9 Geometry Lines, figures, & triangles ppt video
In the diagram above, ∠1 and ∠3 are a pair of vertical angles. Additionally, the endpoints of the chords divide the circle into arcs. Vertical angles are the angles opposite each other when two lines cross. Web when chords intersect in a circle are the vertical angles formed intercept congruent arcs? Vertical angles are formed and located opposite of each.
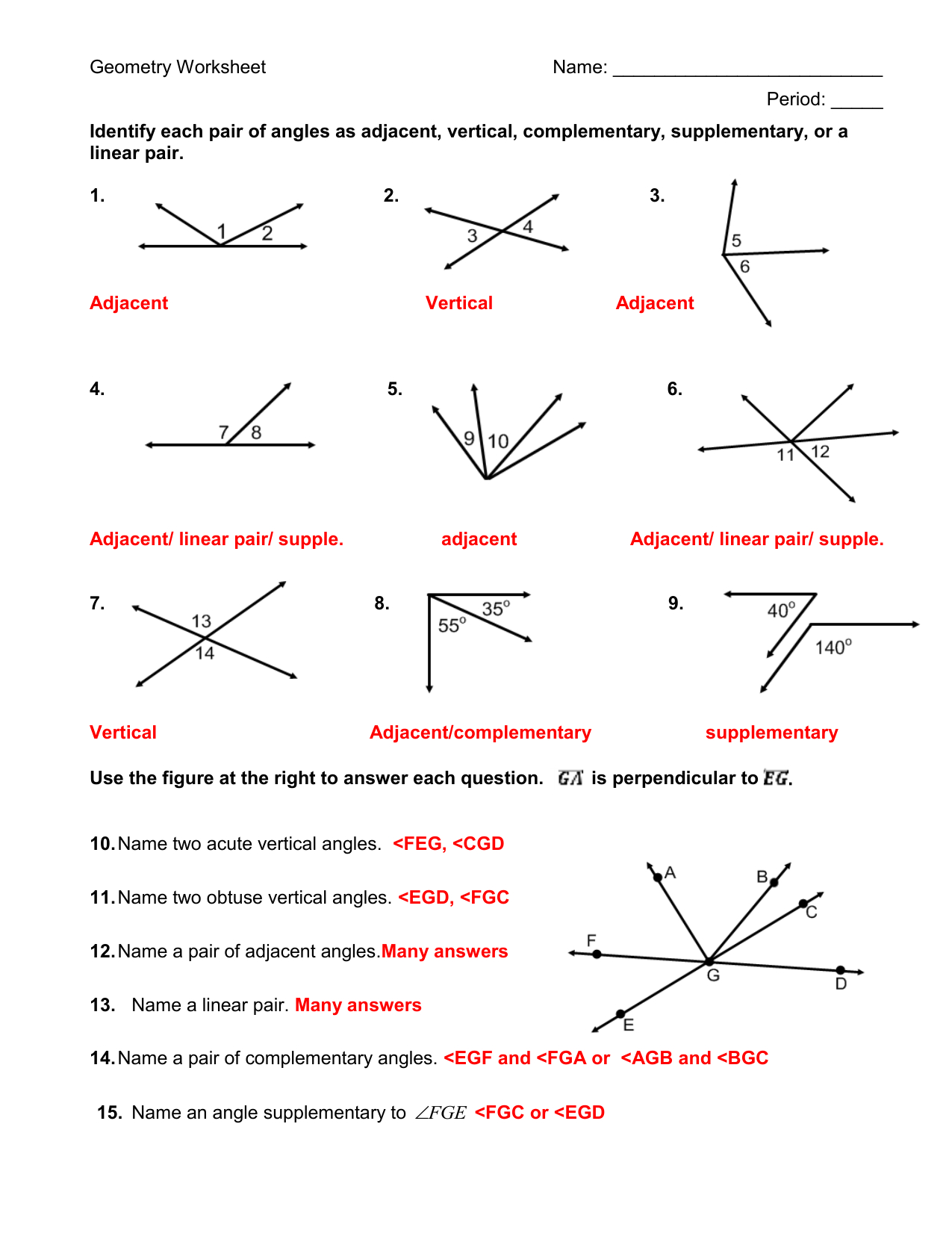
Pairs Of Angles Worksheet Answers —
In the diagram above, chords ab and cd intersect at p forming 2 pairs of congruent vertical angles, ∠apd≅∠cpb and ∠apc≅∠dpb. According to the intersecting chords theorem, if two chords intersect inside a circle so that one is divided into segments of length \(a\) and \(b\) and the other into segments of length \(c\) and \(d\), then \(ab = cd\)..
Vertical Angles Cuemath
I believe the answer to this item is the first choice, true. Web when chords intersect in a circle are the vertical angles formed intercept congruent arcs? Vertical angles are formed and located opposite of each other having the same value. According to the intersecting chords theorem, if two chords intersect inside a circle so that one is divided into.
Intersecting Chords Form A Pair Of Supplementary Vertical Angles
Web intersecting chords theorem: Web i believe the answer to this item is the first choice, true. How do you find the angle of intersecting chords? Vertical angles are formed and located opposite of each other having the same value. I believe the answer to this item is the first choice, true.
Intersecting Chords Form A Pair Of Congruent Vertical Angles
If two chords intersect inside a circle, four angles are formed. Intersecting chords form a pair of congruent vertical angles. Vertical angles are the angles opposite each other when two lines cross. How do you find the angle of intersecting chords? In the circle, the two chords ¯ pr and ¯ qs intersect inside the circle.
How to Prove the Intersecting Chords Theorem of Euclid 7 Steps
In the circle, the two chords ¯ pr and ¯ qs intersect inside the circle. That is, in the drawing above, m∠α = ½ (p+q). Additionally, the endpoints of the chords divide the circle into arcs. Web a simple extension of the inscribed angle theorem shows that the measure of the angle of intersecting chords in a circle is equal.
When chords intersect in a circle, the vertical angles formed intercept
Vertical angles are formed and located opposite of each other having the same value. I believe the answer to this item is the first choice, true. What happens when two chords intersect? Web intersecting chords theorem: If two chords intersect inside a circle, four angles are formed.
Explore the properties of angles formed by two intersecting chords.1
In the diagram above, ∠1 and ∠3 are a pair of vertical angles. That is, in the drawing above, m∠α = ½ (p+q). Vertical angles are formed and located opposite of each other having the same value. Vertical angles are the angles opposite each other when two lines cross. Thus, the answer to this item is true.
Web A Simple Extension Of The Inscribed Angle Theorem Shows That The Measure Of The Angle Of Intersecting Chords In A Circle Is Equal To Half The Sum Of The Measure Of The Two Arcs That The Angle And Its Opposite (Or Vertical) Angle Subtend On The Circle's Perimeter.
Web do intersecting chords form a pair of vertical angles? Vertical angles are formed and located opposite of each other having the same value. Intersecting chords form a pair of congruent vertical angles. In the circle, the two chords ¯ pr and ¯ qs intersect inside the circle.
If Two Chords Intersect Inside A Circle, Four Angles Are Formed.
That is, in the drawing above, m∠α = ½ (p+q). A chord of a circle is a straight line segment whose endpoints both lie on the circle. What happens when two chords intersect? Intersecting chords form a pair of congruent vertical angles.
Web Intersecting Chords Theorem:
In the diagram above, chords ab and cd intersect at p forming 2 pairs of congruent vertical angles, ∠apd≅∠cpb and ∠apc≅∠dpb. ∠2 and ∠4 are also a pair of vertical angles. How do you find the angle of intersecting chords? Web if two chords intersect inside a circle, then the measure of the angle formed is one half the sum of the measure of the arcs intercepted by the angle and its vertical angle.
Thus, The Answer To This Item Is True.
Thus, the answer to this item is true. In the diagram above, ∠1 and ∠3 are a pair of vertical angles. Vertical angles are the angles opposite each other when two lines cross. I believe the answer to this item is the first choice, true.