Parametric Vector Form
Parametric Vector Form - This called a parameterized equation for the same line. Web you can almost always do this, and it's probably the easiest way to go. Where $(x_0,y_0,z_0)$ is the starting position (vector) and $(a,b,c)$ is a direction vector of the line. Web answering your question, you need a parametric vector solution set because the system of equations that is provided to you is underconstrained, that is, the number of variables is greater than the number of equations. Web this is called the parametric vector form of the solution. I have found the cartesian equation, but cannot find the parametric vector form. Web the parametric equations of the line are the components of the vector equation, and have theformx=x0+at, y=y0+bt, andz=z0+ct. But probably it means something like this: It is an expression that produces all points. Example it is sometimes useful to introduce new letters for the parameters.
Polar functions are graphed using polar coordinates, i.e., they take an angle as an input and output a radius! Web this is called the parametric vector form of the solution. A point ( x, y) is on the unit circle if and only if there is a value of t such that these two equations generate that point. Web we can write the parametric form as follows: The symmetric equations of a line are obtained by eliminating the parameter tfrom theparametric equations. Web the one on the form $(x,y,z) = (x_0,y_0,z_0) + t (a,b,c)$. Magnitude & direction to component. Row reduce to reduced row echelon form. Web the parametric equations of the line are the components of the vector equation, and have theformx=x0+at, y=y0+bt, andz=z0+ct. For instance, instead of writing
Polar functions are graphed using polar coordinates, i.e., they take an angle as an input and output a radius! This is also the process of finding the basis of the null space. Web in this section we will derive the vector form and parametric form for the equation of lines in three dimensional space. Matrix, the one with numbers, arranged with rows and columns, is extremely useful in most scientific fields. Web what is a parametric vector form? 1 find a parametric vector form for the solution set of the equation ax~ =~0 for the following matrices a: Web this video explains how to write the parametric vector form of a homogeneous system of equations, ax = 0. A point ( x, y) is on the unit circle if and only if there is a value of t such that these two equations generate that point. Web the parametric form of the solution set of a consistent system of linear equations is obtained as follows. Web we can write the parametric form as follows:
Example Parametric Vector Form of Solution YouTube
Can be written as follows: Row reduce to reduced row echelon form. We turn the above system into a vector equation: Web the parametric form {x = 1 − 5z y = − 1 − 2z. Web this is called the parametric vector form of the solution.
4.2.3 Vector, Cartesian and Parametric Forms YouTube
Can be written as follows: Move all free variables to the right hand side of the equations. (0, −3, 0) − (6, 0, 0) = (−6, −3, 0) ( 0, − 3, 0) − ( 6, 0, 0) = ( − 6, − 3, 0) (0, 0, 2) − (6, 0, 0) =. Web i know the vector form is.
1.5 Parametric Vector FormSolving Ax=b in Parametric Vector Form
Web the parametric form of the solution set of a consistent system of linear equations is obtained as follows. Wait a moment and try again. But probably it means something like this: Web finding vector and parametric equations from the endpoints of the line segment. (a) 1 2 2 4 # (b) 2 66 66 66 4 1 2 3.
Sec 1.5 Rec parametric vector form YouTube
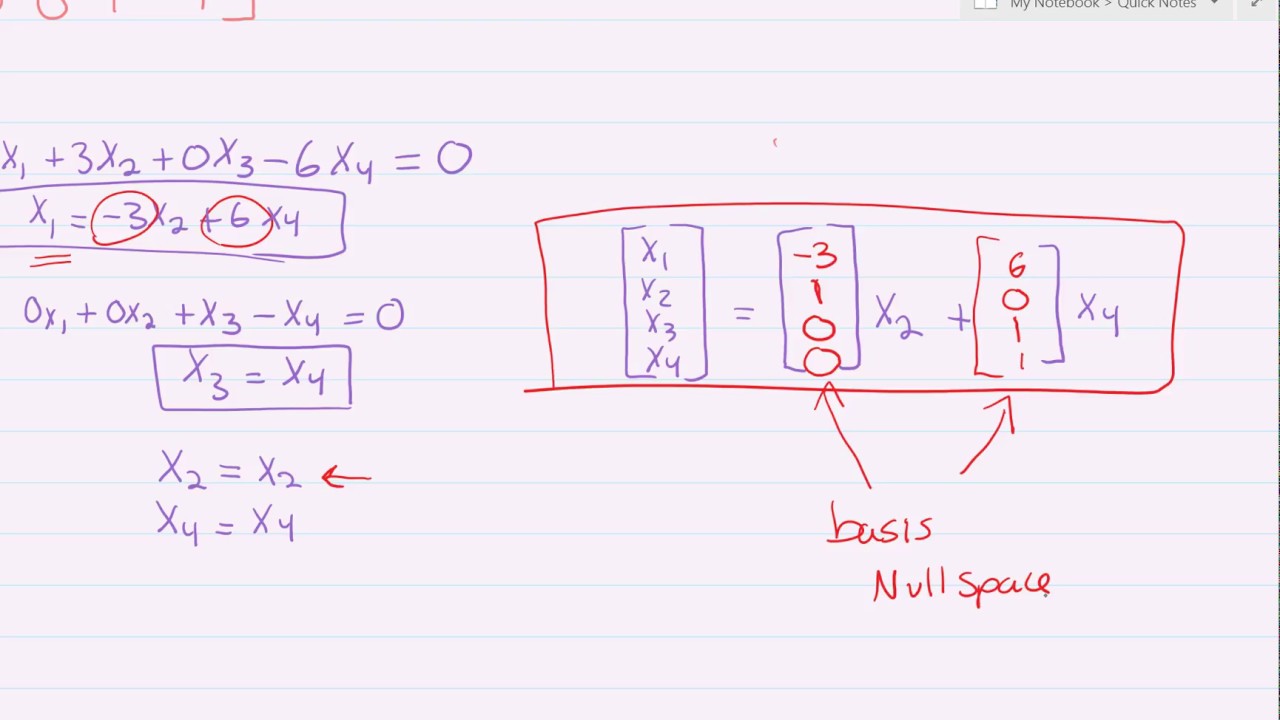
Write the corresponding (solved) system of linear equations. Matrix, the one with numbers, arranged with rows and columns, is extremely useful in most scientific fields. And so, you must express the variables x1 and x2 in terms of x3 and x4 (free variables). This is also the process of finding the basis of the null space. The componentsa, bandcof vare.
Vector Parametric Form Flat Mathematics Stack Exchange
But probably it means something like this: Web this video shows an example of how to write the solution set of a system of linear equations in parametric vector form. Web you can almost always do this, and it's probably the easiest way to go. Where $(x_0,y_0,z_0)$ is the starting position (vector) and $(a,b,c)$ is a direction vector of the.
Parametric Vector at Collection of Parametric Vector
Example it is sometimes useful to introduce new letters for the parameters. Polar functions are graphed using polar coordinates, i.e., they take an angle as an input and output a radius! A point ( x, y) is on the unit circle if and only if there is a value of t such that these two equations generate that point. Web.
Solved Describe all solutions of Ax=0 in parametric vector
I have found the cartesian equation, but cannot find the parametric vector form. 1 find a parametric vector form for the solution set of the equation ax~ =~0 for the following matrices a: Web in this section we will derive the vector form and parametric form for the equation of lines in three dimensional space. But probably it means something.
Parametric Vector Form and Free Variables [Passing Linear Algebra
But probably it means something like this: Note as well that while these forms can also be useful for lines in two dimensional space. Web this video shows an example of how to write the solution set of a system of linear equations in parametric vector form. Web this video explains how to write the parametric vector form of a.
Solved Find the parametric vector form of the solution of
Row reduce to reduced row echelon form. A common parametric vector form uses the free variables as the parameters s1 through s m. Web you can almost always do this, and it's probably the easiest way to go. Web what is a parametric vector form? We emphasize the following fact in particular.
202.3d Parametric Vector Form YouTube
It is an expression that produces all points. Web the parametric form of the solution set of a consistent system of linear equations is obtained as follows. Web this is called a parametric equation or a parametric vector form of the solution. Web the parametric form {x = 1 − 5z y = − 1 − 2z. (a) 1 2.
Web The One On The Form $(X,Y,Z) = (X_0,Y_0,Z_0) + T (A,B,C)$.
{ x 1 = 3 x 2 − 3 x 2 = x 2 + 0. But probably it means something like this: Web the parametric form {x = 1 − 5z y = − 1 − 2z. Web this is called the parametric vector form of the solution.
Write The Corresponding (Solved) System Of Linear Equations.
Web you can almost always do this, and it's probably the easiest way to go. Where $(x_0,y_0,z_0)$ is the starting position (vector) and $(a,b,c)$ is a direction vector of the line. 1 find a parametric vector form for the solution set of the equation ax~ =~0 for the following matrices a: We will also give the symmetric equations of lines in three dimensional space.
Terminology Is Not Altogether Standard So Check With Your Instructors.
It is an expression that produces all points. Web this is called a parametric equation or a parametric vector form of the solution. X1 = 1 + 2λ , x2 = 3 + 4λ , x3 = 5 + 6λ , x 1 = 1 + 2 λ , x 2 = 3 + 4 λ , x 3 = 5 + 6 λ , then the parametric vector form would be. Note as well that while these forms can also be useful for lines in two dimensional space.
If You Have A General Solution For Example.
The symmetric equations of a line are obtained by eliminating the parameter tfrom theparametric equations. Learn about these functions and how we apply the concepts of the derivative and the integral on them. The componentsa, bandcof vare called thedirection numbers of the line. Write the system as an augmented matrix.