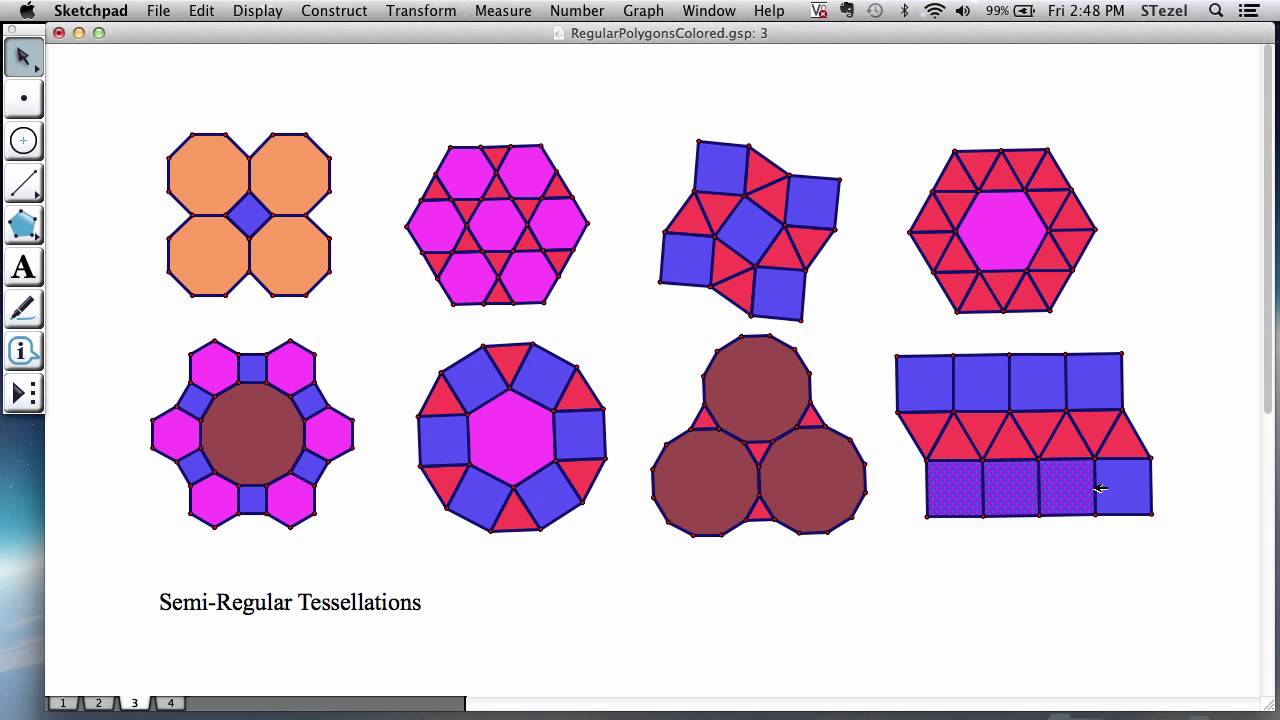
Which Of The Following Polygons Can Form A Regular Tessellation
Which Of The Following Polygons Can Form A Regular Tessellation - They are formed by two or more types of regular polygon, each with the same side length each. Determine whether the given regular polygon(s) can be used to form a tessellation. [6] [7] polygons in these meet at a point with no gap or overlap. Web tessellations that are made with just one shape are called monohedral tiling, or regular tessellations. Regular tessellation a regular tessellation is made up of regular congruent polygons. Web you can similarly check that, just like pentagons, any regular polygon with 7 or more sides doesn’t tessellate. Web which of the following polygons can form a regular tessellation? Web a regular tessellation is a design covering the plane made using 1 type of regular polygons. This means that the only regular polygons that tessellate are. So, equilateral triangle cannot be used to.
Determine whether the given regular polygon(s) can be used to form a tessellation. Web classifying tessellations there are 3 types of tessellations. [6] [7] polygons in these meet at a point with no gap or overlap. Regular tessellation a regular tessellation is made up of regular congruent polygons. It is only with these three shapes. Web which of the following polygons can form a regular tessellation? They are formed by two or more types of regular polygon, each with the same side length each. Determine whether the given regular polygon(s) can be used to form a tessellation. Web a regular tessellation is a design covering the plane made using 1 type of regular polygons. Web geometry geometry questions and answers which of the following polygons can form a regular tessellation?
Invite students to choose a corner point on the triangle tessellation. Web tessellations that are made with just one shape are called monohedral tiling, or regular tessellations. It is only with these three shapes. Determine whether the given regular polygon(s) can be used to form a tessellation. Determine whether the given regular polygon(s) can be used to form a tessellation. Regular tessellation a regular tessellation is made up of regular congruent polygons. These types of tiling can be made either with regular. Those made up of equilateral triangles, squares, or regular hexagons. Web which of the following polygons can form a regular tessellation? Web other math questions and answers.
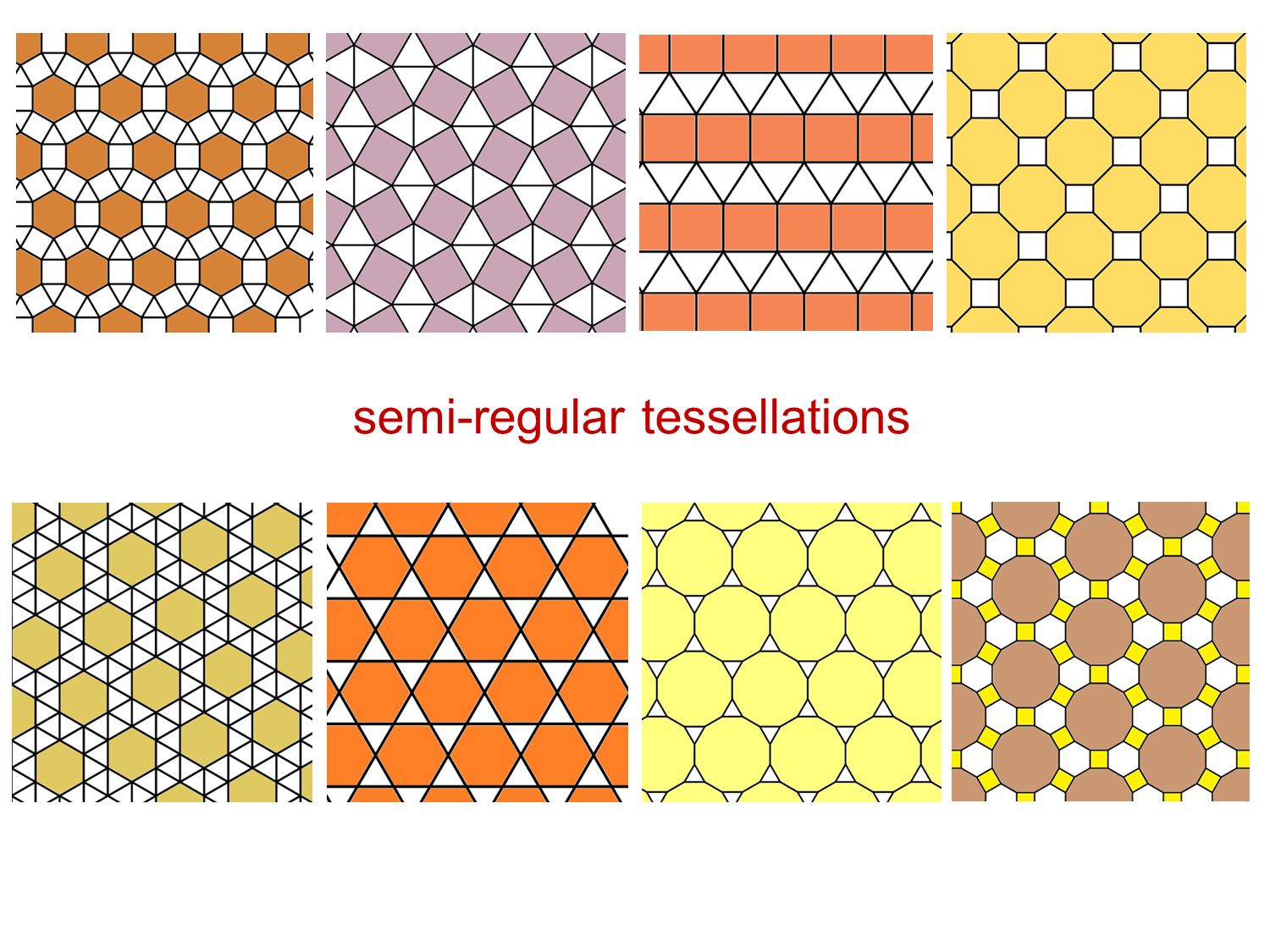
MEDIAN Don Steward mathematics teaching semi regular tessellations
Web classifying tessellations there are 3 types of tessellations. Web to form a regular tessellation, the angle measure of a regular polygon must be a divisor of 360 ∘ ^{\circ} ∘ in this case, regular polygon is octagon and each angle of octagon. Regular polygons tessellate if the interior angles can be added together to make 360°. Web a regular.
Which of the following polygons can form a regular tessellation
Web you can similarly check that, just like pentagons, any regular polygon with 7 or more sides doesn’t tessellate. Web to form a regular tessellation, the angle measure of a regular polygon must be a divisor of 360 ∘ ^{\circ} ∘ in this case, regular polygon is octagon and each angle of octagon. Web geometry geometry questions and answers which.
Regular Polygons in a Tessellation Triangles, Squares, Hexagons, and
Web tessellations that are made with just one shape are called monohedral tiling, or regular tessellations. They are formed by two or more types of regular polygon, each with the same side length each. Determine whether the given regular polygon(s) can be used to form a tessellation. Web geometry geometry questions and answers which of the following polygons can form.
Tessellations (4) SemiRegular Tessellations YouTube
They are formed by two or more types of regular polygon, each with the same side length each. Web the regular polygons that can be used to form a regular tessellation are an equilateral triangle, a square, and a regular hexagon. Web a tessellation is a pattern created with identical shapes which fit together with no gaps. This means that.
10.6 Video Investigation "Which Regular Polygons Tessellate?" YouTube
Web which of the following polygons can form a regular tessellation? Web a regular tessellation is a design covering the plane made using 1 type of regular polygons. Web check all that apply. Web there are only three regular tessellations: Web a tessellation is a pattern created with identical shapes which fit together with no gaps.
Is there a 9 Sided Shape?
Web there are only three regular tessellations: Determine whether the given regular polygon(s) can be used to form a tessellation. It is only with these three shapes. Web here is a table to prove why there are only three regular polygons that create regular tessellations: Web geometry geometry questions and answers which of the following polygons can form a regular.
Make maths more creative. Hollie Ferguson ePortfolio
So, equilateral triangle cannot be used to. Web to form a regular tessellation, the angle measure of a regular polygon must be a divisor of 360 ∘ ^{\circ} ∘ in this case, regular polygon is octagon and each angle of octagon. Web you can similarly check that, just like pentagons, any regular polygon with 7 or more sides doesn’t tessellate..
Actv regular tessellations
Web here is a table to prove why there are only three regular polygons that create regular tessellations: Web other math questions and answers. Web classifying tessellations there are 3 types of tessellations. Web to form a regular tessellation, the angle measure of a regular polygon must be a divisor of 360 ∘ ^{\circ} ∘ in this case, regular polygon.
MEDIAN Don Steward mathematics teaching semi regular tessellations
It is only with these three shapes. Regular tessellation a regular tessellation is made up of regular congruent polygons. Determine whether the given regular polygon(s) can be used to form a tessellation. Regular polygons tessellate if the interior angles can be added together to make 360°. Those made up of equilateral triangles, squares, or regular hexagons.
Tessellations (2) Regular Polygon Construction YouTube
Web which of the following polygons can form a regular tessellation? Those made up of equilateral triangles, squares, or regular hexagons. It is only with these three shapes. Web here is a table to prove why there are only three regular polygons that create regular tessellations: This means that the only regular polygons that tessellate are.
Web Check All That Apply.
They are formed by two or more types of regular polygon, each with the same side length each. Web the regular polygons that can be used to form a regular tessellation are an equilateral triangle, a square, and a regular hexagon. Invite students to choose a corner point on the triangle tessellation. Web a regular tessellation is a design covering the plane made using 1 type of regular polygons.
Those Made Up Of Equilateral Triangles, Squares, Or Regular Hexagons.
Web other math questions and answers. Regular polygons tessellate if the interior angles can be added together to make 360°. These types of tiling can be made either with regular. Web geometry geometry questions and answers which of the following polygons can form a regular tessellation?
Web To Form A Regular Tessellation, The Angle Measure Of A Regular Polygon Must Be A Divisor Of 360 ∘ ^{\Circ} ∘ In This Case, Regular Polygon Is Octagon And Each Angle Of Octagon.
Web a tessellation is a pattern created with identical shapes which fit together with no gaps. [6] [7] polygons in these meet at a point with no gap or overlap. Question 3 of 33 which of the following polygons can form a regular tessellation? This means that the only regular polygons that tessellate are.
Web You Can Similarly Check That, Just Like Pentagons, Any Regular Polygon With 7 Or More Sides Doesn’t Tessellate.
So, equilateral triangle cannot be used to. Web tessellations that are made with just one shape are called monohedral tiling, or regular tessellations. Determine whether the given regular polygon(s) can be used to form a tessellation. Web classifying tessellations there are 3 types of tessellations.